[딥러닝/머신러닝] Logistic Regression, Sigmoid, Binary Classification에 대하여

일상 속 풀고자하는 많은 문제 중에서는 두 개의 선택지 중에서 정답을 고르는 문제가 많습니다. 예를 들어 시험을 봤는데 이 시험 점수가 합격인지 불합격인지가 궁금할 수도 있고, 어떤 메일을 받았을 때 이게 정상 메일인지 스팸 메일인지를 분류하는 문제도 그렇습니다. 이렇게 둘 중 하나를 결정하는 문제를 이진 분류(Binary Classification)라고 합니다. 그리고 이런 문제를 풀기 위한 대표적인 알고리즘으로 로지스틱 회귀(Logistic Regression)가 있습니다.

 

목차

1. 이진분류 (Binary Classification)
2. 시그모이드 함수 (Sigmoid)
3. 비용함수 (Cost function)

 

 

---

 

이진분류 (Binary Classification)

둘 중 하나의 선택지 중에서 정답을 고르는 이진 분류 문제는 직선으로 표현하는 것이 적절하지 않다.

이러한 x와 y의 관계를 표현하기 위해서는 직선을 표현하는 함수가 아니라 S자 형태로 표현할 수 있는 함수가 필요합니다. 직선을 사용할 경우 보통 분류 작업이 제대로 동작하지 않습니다.

이번 예제의 경우 실제값. 즉, 레이블에 해당하는 y가 0 또는 1이라는 두 가지 값만을 가지므로, 이 문제를 풀기 위해서 예측값은 0과 1사이의 값을 가지도록 합니다. 0과 1사이의 값을 확률로 해석하면 문제를 풀기가 훨씬 용이해집니다. 최종 예측값이 0.5보다 작으면 0으로 예측했다고 판단하고, 0.5보다 크면 1로 예측했다고 판단합니다.

 

출력이 0과 1사이의 값을 가지면서 S자 형태로 그려지는 함수로 시그모이드 함수(Sigmoid function)가 있습니다.

 

 

시그모이드 함수(Sigmoid function)

시그모이드 함수는 종종 σ로 축약해서 표현하기도 합니다. 로지스틱 회귀를 풀기 위한 가설을 세워봅시다.

https://wikidocs.net/22881

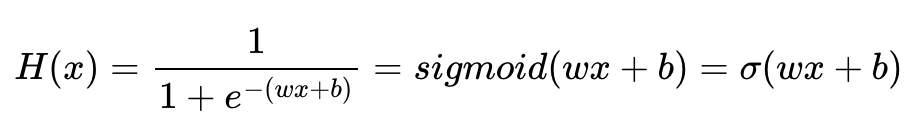
여기서 e(e=2.718281...)는 자연 상수라 불리는 숫자입니다. 여기서 구해야할 것은 여전히 주어진 데이터에 가장 적합한 가중치 w(weight)와 편향 b(bias)입니다. 인공 지능 알고리즘이 하는 것은 결국 주어진 데이터에 적합한 가중치 w와 b를 구하는 것입니다.

 

https://wikidocs.net/22881

Sigmoid 함수는 위의 그래프와 같이 출력값을 0과 1사이의 값으로 조정하여 반환한다. 마치 S자의 모양을 연상시킵니다.

 

w의 변화에 따른 그래프의 변화

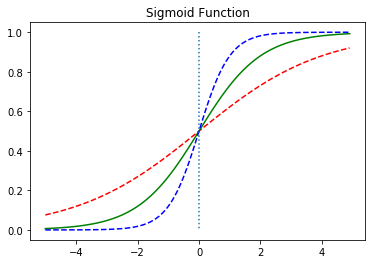
가중치 w의 값에 따라 모양이 변하며,

w의 값이 0.5일때 빨간색선, w의 값이 1일때는 초록색선, w의 값이 2일때 파란색선이 나오도록 하였습니다. w의 값에 따라 그래프의 경사도가 변합니다. 선형 회귀에서 직선을 표현할 때, 가중치 w는 직선의 기울기를 의미했지만 여기서는 그래프의 경사도를 결정합니다. w의 값이 커지면 경사가 커지고 w의 값이 작아지면 경사가 작아집니다.

 

b의 변화에 따른 그래프의 변화

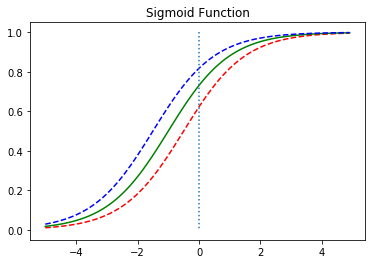
위 그래프는 b값에 따라서 그래프가 이동하는 것을 보여줍니다.

 

이처럼, 시그모이드 함수는 입력값이 커지면 1에 수렴하고, 입력값이 작아지면 0에 수렴합니다. 0부터의 1까지의 값을 가지는데 출력값이 0.5 이상이면 1(True), 0.5이하면 0(False)로 만들면 이진 분류 문제를 풀기 위해서 사용할 수 있습니다.

 

 

 

 

비용함수 (Cost function)

로지스틱 회귀 또한 경사 하강법을 사용하여 가중치 w를 찾아내지만, 비용 함수로는 평균 제곱 오차를 사용하지 않습니다. 평균 제곱 오차를 로지스틱 회귀의 비용 함수로 사용했을 때는 좋지 않은 로컬 미니멈에 빠질 가능성이 지나치게 높아 문제 해결이 어렵습니다.

 

로지스틱 회귀라는 문제에서 가중치 w를 최소로 만드는 적절한 새로운 비용 함수를 찾아야 합니다. 가중치를 최소화하는 아래의 어떤 함수를 목적 함수라고 합시다. w는 목적 함수(objective function)를 의미합니다.

 

시그모이드 함수는 0과 1사이의 y값을 반환합니다. 이는 실제값이 0일 때 y값이 1에 가까워지면 오차가 커지며 실제값이 1일 때 y값이 0에 가까워지면 오차가 커짐을 의미합니다. 그리고 이를 반영할 수 있는 함수는 로그 함수를 통해 표현 가능합니다.

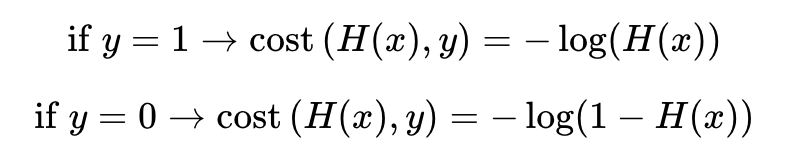
y의 실제값이 1일 때 −log(H(x)) 그래프를 사용하고 y의 실제값이 0일 때 -log(1-H(x)) 그래프를 사용해야 합니다. 위의 두 식을 그래프 상으로 표현하면 아래와 같습니다.

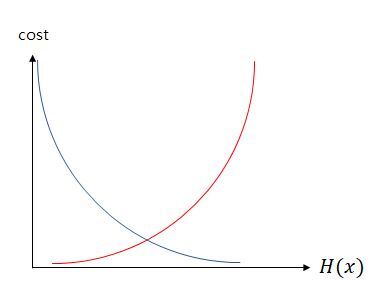
따라서, 비용 함수를 식으로 나타내면

비용함수, Cost function

결과적으로 목적 함수는 

목적함수, Objective function

 

 

 

 

 

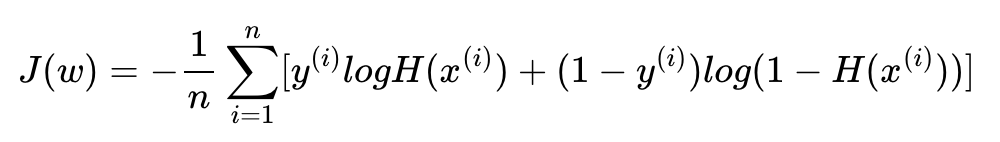
<딥 러닝을 이용한 자연어 처리 입문> E-book을 보고 공부한 내용 + 인터넷 자료 + 학부에서 배운 강의 내용을 정리한 자료입니다.

https://wikidocs.net/21679

06-01 머신 러닝이란(What is Machine Learning?)