| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- FlatList
- 그래프
- 상담원 인원
- 이진탐색
- LV3
- TouchableWithoutFeedback
- 17089
- 괄호제거
- 프로그래머스
- 큐
- 그리디
- useHeaderHeight
- ReactNative
- 3079
- 복잡도 측정
- 11831
- 이분탐색
- 시간초과해결
- 2800
- PYTHON
- 골드5
- React #새파일생성
- 브루트포스
- KeyboardAvoidingView
- 딥러닝
- 자료구조
- 머신러닝
- 실버1
- 백준
- 수정렬하기4
- Today
- Total
지니 코딩일기
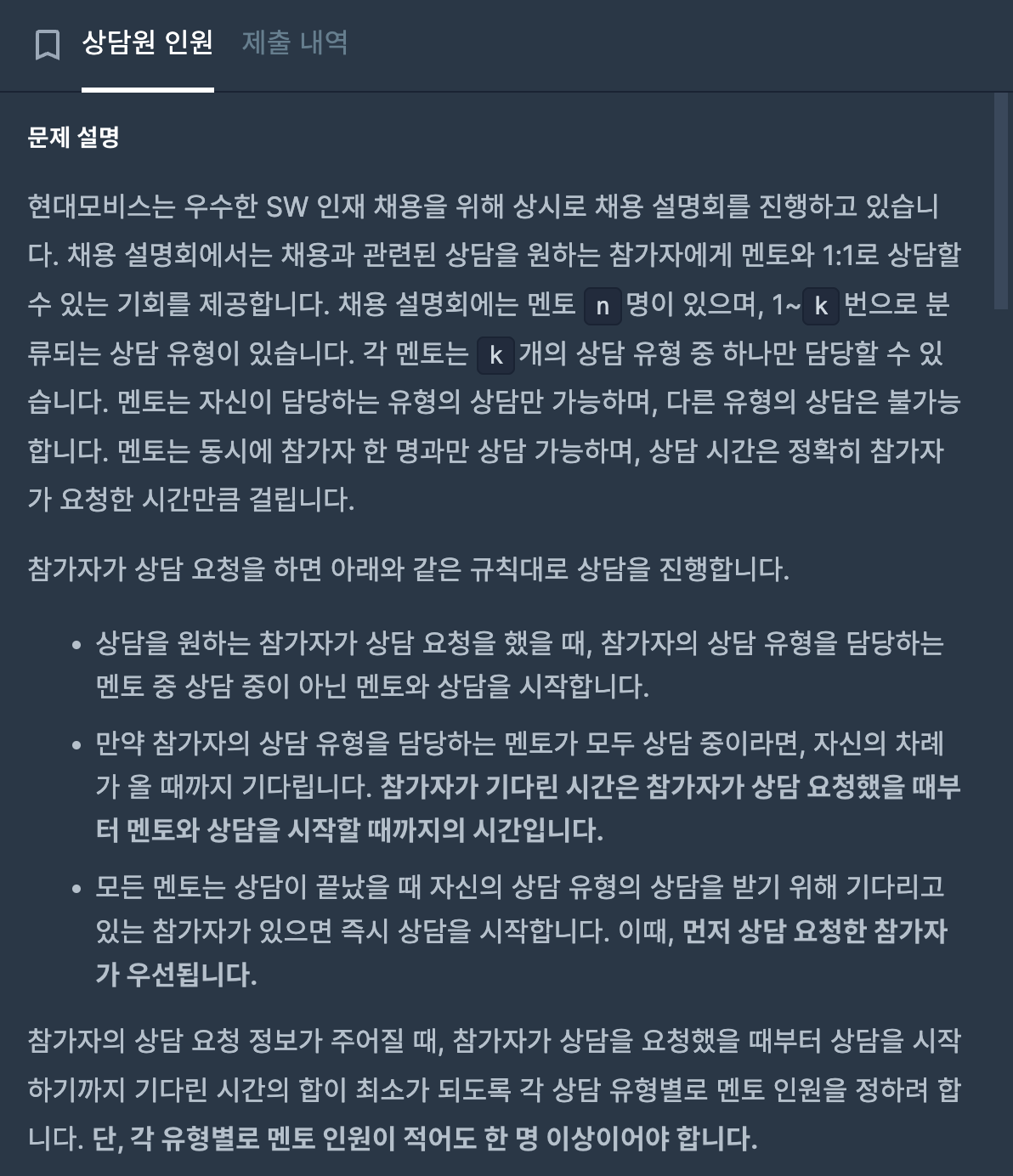
[프로그래머스] #상담원 인원 (Python) 본문
2024/3/7
lv3
https://school.programmers.co.kr/learn/courses/30/lessons/214288#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
🔎 분석
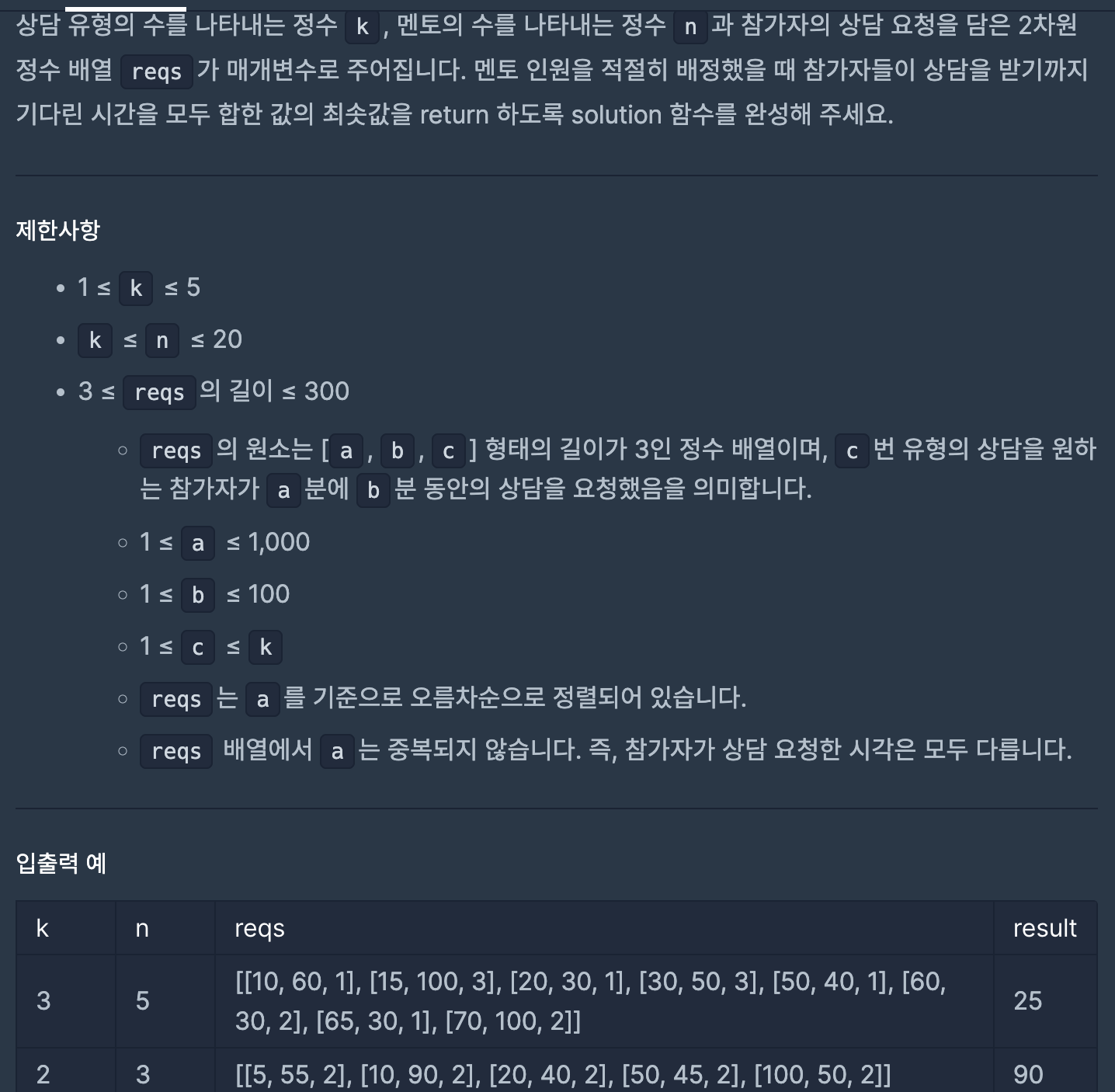
n명이 k개의 유형별로 반드시 1명씩은 배치되어야 하기 때문에, k명을 배치한 후, n-k명을 어떻게 배치할 지 고민했다.
처음에는 1명씩 배치한 후, 기다린 시간이 큰 순서대로 1명씩 추가 배치하려 했다.
하지만, 이렇게 하는 경우, 반례가 있었다.
그래서 for문을 돌려서 각 유형을 선택했을 때 결과를 비교하고, 기다린 시간의 총합이 최소가 되는 것을 고르도록 하였다.
재귀, while문 상관 없었지만, 이번에는 재귀로 구했다.
그리고 추가로, 이번에도 문제를 제대로 해석하지 않아서 시간이 매우 오래 걸렸다.
상담이 끝나는 순서대로 무조건 진행해야 했는데, 그 부분을 다르게 구했었다 ...
✏️ 과정
1.
reqs를 유형별로 분류하여 kinds 배열에 저장한다
2.
find_total 함수를 통해 mentos 배열을 구한다.
mentos = [mento....]
mento = [끝나는 시간, 기다린 시간]
➡️ 각 mento별로 끝나는 시간, 기다린 시간을 저장해주었다
3.
find_total 함수를 통해 기다린 시간의 총합을 구한다.
4.
재귀함수인 recursion 함수를 통해 기다린 시간의 총합이 최소가 되도록 하는 인원 배치를 구한다.
📍느낀점
첫 코드는 정말 지저분했는데, 다시 지우고 새로 짜다보니까 좀 더 깔끔한 코드를 구현하게 됐다.
짜다가 막히면 다시 처음부터 짜보기 !
💻 코드
import copy
INF = 99999
answer = 0
def recursion(kinds, mentos, total, n):
global answer
if n==0:
if total < answer:
answer = total
return
mini_mentos = mentos
mini_total = total
for i in range(1, len(kinds)):
new_mentos = copy.deepcopy(mentos)
# 초기화
for j in range(len(new_mentos[i])):
new_mentos[i][j] = [0, 0]
new_mentos[i].append([0, 0]) # 새로운 멘토 추가
result = find_total(i, kinds, new_mentos) # 결과 구하기
if result <= mini_total:
mini_mentos = new_mentos
mini_total = result
recursion(kinds, mini_mentos, mini_total, n-1)
return
def find_total(mode, kinds, mentos):
# mode==0 : 전체 구하기
# mode==1,2,3 : 1,2,3 중 하나 구하기
if mode==0:
for kind in kinds:
for req in kind:
mini = INF
mini_idx = 0
# 상담이 끝나는 순서대로 무조건 진행!!
# mento=[끝나는 시간, 기다린 시간]
mentos[req[2]].sort(key=lambda x:x[0])
mento = mentos[req[2]][0]
if mento[0] <= req[0]:
# 상담 시작 시간 >= 이전 상담 종료 시간이므로, 상담 진행, 상담 종료 시간=시작+진행시간
mento[0] = req[0] + req[1] # 상담 종료 시간
else:
# 상담 시작 시간 < 이전 상담 종료 시간이므로, 기다려서 진행한다
mento[1] += mento[0] - req[0] # 기다린 시간
mento[0] += req[1] # 상담 종료 시간
else:
for req in kinds[mode]:
mentos[req[2]].sort(key=lambda x:x[0])
mento = mentos[req[2]][0]
if mento[0] <= req[0]:
# 상담 시작 시간 >= 이전 상담 종료 시간이므로, 상담 진행, 상담 종료 시간=시작+진행시간
mento[0] = req[0] + req[1] # 상담 종료 시간
else:
# 상담 시작 시간 < 이전 상담 종료 시간이므로, 기다려서 진행한다
mento[1] += mento[0] - req[0] # 기다린 시간
mento[0] += req[1] # 상담 종료 시간
total = 0
for i in range(len(mentos)):
for j in range(len(mentos[i])):
total += mentos[i][j][1]
return total
def solution(k, n, reqs):
global answer
answer = 0
# 유형별로 분리
# DFS로 돌면서 인원을 추가하고, 가장 결과가 작은 것을 채택
kinds = [[] for _ in range(k+1)]
mentos = [[[0, 0]] for _ in range(k+1)]
for req in reqs:
kinds[req[2]].append(req)
answer = find_total(0, kinds, mentos)
recursion(kinds, mentos, answer, n-k)
return answer'알고리즘 > 코테 준비' 카테고리의 다른 글
| [프로그래머스] #과제 진행하기 (Python) (2) | 2024.03.05 |
|---|---|
| [백준] Python 시간초과 해결 방법 (0) | 2023.08.14 |
| DFS/BFS에 대해 (0) | 2023.04.12 |
| DFS/BFS에 대해 - 스택, 큐, 재귀함수란 ? (0) | 2023.04.12 |
| 알고리즘의 복잡도 (0) | 2023.04.10 |


